명제파트 수능 기출문제 질문
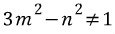 이다
이다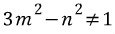 이다의 '이' 인데요..)
이다의 '이' 인데요..)0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-
시발점 질문.. 0
다른 쌤들 개념강의는 20-30강인데 시발점은 무슨 50,80강… 뉴런도 뉴런나름...
-
재수하면 과탐 오를까요 ? 생지 했었는데 생명 유전 너무 어려워서 힘들었는데...
-
수학 개념 복습 0
개념 다 까먹어서 복습하려는데 한완수 좋아요? 감 다잃어서
-
정시인데 리로스쿨 한달 밀려서 무단결석 두개 끄였는데 이거 출결 고려대 ~중경외시...
-
오운완 13
오늘 덤벨 못들고 호에에거리니까 옆에 아저씨한테 자세랑 인체구조에 대해서 10분간 강의들음..
-
널 못 잊을 나보다 사랑했던 만큼 아파할 너이기에
-
22수능이 147이고 23수능이 145다 즉 만표는 끼야미 통통이 아가들이 정하는 것이다.
-
2024수능 2025 수능 서성한 공대 못 뚫으면 그냥 시도 자체도 안함뇨
-
보통 고2, 고3 땐 선택과목 따라서 수업을 듣잖아여 그러면 각 반의 성비가 다르게...
-
수학 인강들을려고 하는데요… 이미지 현우진 고민중입니다 나중에 +a로 4공법도...
-
올수 국어 수학 33떳는데 2월까진 국어수학 베이스 잡는데 집중하고 3월에...
-
뭔가파격적인 글을 이제 못쓰겟음.... 왜냐면 에타에선 그랬다간 큰일나니까 죄다 순한맛이되
-
행복했다...
-
2014-15년쯤에 3700명 의전원 포함해서 뽑는데 지금 3000명 애초에 못해도...
-
과민성대장증후군 관련 설문조사 (GS25 1만원권 기프티콘 지급) 1
안녕하세요. 저희는 과민성대장증후군 관련 제품을 개발 중인 연세대와 고려대 학생으로...
-
성논 공학 0
성대 논술 공학계열 여러분들 얼마나 쓰셧나요
-
토정비결에 대하여.. 역사 알아봤습니다^^. 적고나니 비문학 지문 같네요!...
-
순위도 좋고 그냥 경기권 대학 중 아는 대학 막 던져주고 가주세요..
-
콱
-
D-7 5
-
과외알바를 생각하시는 분들을 위한 매뉴얼&팁입니다. 미리 하나 장만해두세요~~...
-
새벽에 올린글에 댓글도 많이달아주시고 쪽지도 많이보내주셔서 감사합니다ㅎㅎ 20살에...
-
언미생지 입니다
-
컨설팅 0
크럭스/피오르 대기 뭐 신청하지.. 강대꺼만 받기는 좀 두렵다
-
사탐런 과목 찾는데 전적대 경제라 경제하려고 했는데 다들 뜯어말리네...
-
개 피곤하다 1
-
오프라인으로 살려는데
-
제 사촌동생이 이번 수능에서 55455 받아왔습니다. 근데 제가 이 라인을 잘...
-
4번 문제가 마냥 쉬웠다는 것은 아니지만 이번 동사에서 1등급을 가르는 문제는...
-
애들이 막 트리에 한마디씩 달아주라는 링크 올리네
-
99는 죽어도 안되나..
-
동국(경영) Vs 숙명(경제)Vs 인하(아태) 어디가 좋을까요? 6
동국 경영 숙명 경영 인하 아태물류 중에 어디로 결정하는 것이 좋을까요?
-
딱히 특별한건 없고… 2024 6월 백분위 100/ 9월 98 / 수능 99...
-
반수 결심하면 1
대학생활 제대로 못즐기겠죠??? 남들처럼 놀고 연애하고 이런거 시작도 못하나요?
-
와 저 졸림 0
저 대신 숙면 취해주실분
-
미적틀 96에게 3
백분위 100을 내놓아라
-
삼반수 예정이고 작수 4 올해 수능 85점(확통)입니다... 찍맞 +8점이 좀...
-
지옥2 보기 2
-
삼전 씨발놈들아 0
왜 자꾸 떨어져서 단타도 못치게 하냐고.
-
수2 문제 질문 1
수2문제인데 피램국어에있어서 ㅋㅋㅋㅋㅋ 풀어봄 답 5번이 맞을까요??답 5번이...
-
현역 32411 5
영어를 너무 망쳤는데 이 성적이면 어디까지 가능한가요? 중경외시 가고 싶은데...
-
미적분학 교재는 3
보통 뭘 쓰나요 겨울에 공부 좀 해보려고하는데
-
그건 바로 애니메이트와의 거리임
-
탐구 선택 1
물지하려다가 탐구 점수가 너무 낮아서 사문정법으로 런할까 고민중입니다 사탐두개...
-
님아. 0
-
올해 대학 붙여놓고 1학기 하고 군입대 후 군수 vs 1학기 후 휴학반수 한뒤...
-
지고쿠 지고쿠 8
-
참 좋아하는 과목이고 이걸로 돈도 벌지만 나는 출제도 하고 과외도 하지만 내...
-
수2 극한 7
y= 1/절댓값(x-1)에서, 발산인 이유가 x=1에서 만나지 않아서 인가요...










































[배경지식]
p →q를 부정하면 p and ~q가 됩니다.
예를 들어서
(p)국회의원은 (q)정신병자다.
라는 명제를 부정하고 싶다면
(p)국회의원이면서 (~q)정신병자가 아닌 경우를 찾아내면 돼요.
귀류법이란
p and ~q를 가정하고 모순을 이끌어내는 논증의 기술입니다.
모순의 모양이 어떠해야 한다고 단정지어 말할 수는 없어요.
p and ~p일수도 있고, q and ~q일수도 있고
어떤 방식이건 모순을 이끌어내면 되는데요.
반면 대우증명법은
p→q를 증명하기 위해서
~q라 가정하고 ~p를 이끌어내는 방법을 의미합니다.
질문자는 대우증명법과 귀류법을 좀 믹스해서 이해하고 있네요.
[질문1에 대한 답변]
구조를 분석하기 위해서 다음과 같이 기호를 붙여보겠습니다.
(p) 3m²-n²=1
(q) 정수순서쌍(m,n)
이제 문제에서 증명하고자 하는 명제는
(p and q)는 존재하지 않는다.
로 표현할 수 있습니다. 조건문(→)이 아니라 and로 두 조건이 서로 연결되어 있다는 점을 주의해야겠지요.
[질문2에 대한 답변]
제시문에서는 주어진 명제를 증명하기 위해서
p and q를 가정하고 모순(0 = 1 or 2 )을 이끌어내고 있습니다.
앞서 간단히 언급한 것처럼
질문자는 and로 연결된 부분을 조건문(→)으로 이해해서 혼란을 느끼고 있네요.
상세한 답변 고맙습니다..이해가 잘 되네요.